A Genealogical Look at Shared Ancestry on the X Chromosome
My article with Steve Mount and Graham Coop, A Genealogical Look at Shared Ancestry on the X Chromosome has been published in Genetics. In the spirit of both outreach and continuing Graham’s terrific series of blog posts1 on genetic genealogy, I’m writing about our paper on X chromosome genealogy and recent ancestry. Before diving into the details of X chromosome ancestry work, I’ll review the concepts of genealogies and ancestry. Then, in the next section we’ll look at how one’s genetic ancestors —the subset of ancestors that you share genetic material with— vary back through the generations. With these concepts reviewed, we’ll look at the genealogy that includes all of our X ancestors, which due to the special inheritance pattern of the X chromosome is only a subset of one’s genealogy. The embedded X genealogy has some properties that impact how segments of DNA are shared between individuals with recent common ancestry (e.g. 6th degree cousins), which we look at through a simple probability model. Finally, we’ll look at what we can learn about the relationships of individuals that share sections of their X chromosome due to sharing a recent common ancestor.
Genealogies
Each human, as a sexually reproducing species with two sexes, has two parents. You have two parents, four grandparents, eight great-grandparents, 16 great-great grandparents, and \(k\) generations back have \(2^k\) great\((k-2)\) grandparents, and in general \(2^k\) ancestors \(k\) generations back. An example genealogy back five generations is shown below:

Of course, these genealogical ancestors are not necessarily all distinct individuals; as you go further back through the generations, some of these \(2^k\) individuals aren’t unique—they’re the same person. Intuitively, this occurs when one’s two parents are actually related some number of generations back. For example, one’s two parents could be 9th degree cousins—e.g. if we assume a generation time of about 30 years, this means these parents shared an ancestor around 270 years ago. This phenomenon is known as pedigree collapse, and it’s the same thing as inbreeding. The further back through the generations you go back, pedigree collapse must happen—it’s exceedingly unlikely that 20 generations ago, your 1,048,576 ancestors are all distinct.2 While pedigree collapse definitely occurs, throughout the rest of this blog post (and in our paper) we ignore it, as we model ancestry that’s recent enough where pedigree collapse isn’t a large problem.
Genetic Ancestry
Since each of us have two parents, we receive ½ of our autosomal (i.e. not including the sex chromosomes) genetic material from each parent. We share ½ of our genome with our mother, and ½ with our father. Since your mother shares ½ her genetic material with her two parents, you share ¼ of your genetic material with each grandparent. In general, on average you’ll share ½k of your genome with an ancestor \(k\) generations in the past. Since the number of crossovers per chromosome is limited, close relatives are likely to share large contiguous segments of their genetic material; a beautiful visualization of this is Morgan’s 1916 illustration of crossing over:

When we look at how much DNA two relatives share, we see it occurs in large blocks like the black and white segments above. For example, using 23andme’s Ancestry Tools I can see how much DNA my grandmother and I share—around 14 Morgans spread across 21 long segments. Essentially, the fact that on average only one crossover occurs per chromosome3 per generation limits how much the genome is broken up through the generations. While on average ¼ of my DNA should be identical to my grandmother’s DNA (we say such genetic material is identical by descent) there’s variance around this ¼ because the genome is of finite length and recombination is limited. In other words, the fraction of my genome that derives from my grandmother isn’t like randomly sampling 6.6 billion marbles independently (the number of basepairs in a diploid human genome), a quarter of which are colored red (i.e. come from my grandmother) and the rest white (i.e. come from my other ancestors). Rather, a more appropriate model is that these marbles are connected by string that is cut and reattached (much like Morgan envisioned in his illustration)—leading recent ancestry to be blocky and segmented.
Currently, there are computational methods (e.g. Browning and Browning, 2011) that take polymorphism datasets and using probabilistic models, identify large identical by descent (IBD) regions shared between individuals—it’s programs like these that services like 23andme use to infer how far back your relatives share ancestry with you. So if we wish to take genomic datasets and understand the large shared segments between relatives due to their shared ancestry4 we need a more appropriate mathematical model than the simple model of sampling marbles. Numerous probabilists and statistical geneticists have tackled this using probability theory and stochastic processes (Donnelly 1983; Huff et al., 2011; Thomas et al., 1994). Some of the mathematical details are rather complex (leading to fun conceptualizations like “a random walk on a hypercube”), but the underlying model can be simplified considerably.
Each generation, we can imagine that a random number \(B\) of crossovers breaks the 22 human autosome, creating \(B+22\) segments. As in Morgan’s original illustration (above), this leads to complementary gametes, with alternating paternal and maternal segments (the black and white segments in the rightmost figure). Mathematically, tracking these alternate segments is a bit tricky, so we can approximate the process by imaging that each of the segments is passed on to the next generation with probability ½—a flip of a fair coin. Since we don’t actually know how many breakpoints have occurred, we model them as a random process. In our case, we use the Poisson distribution5 to assign a probability to the event that some number of breakpoints \(B=b\) occurs. This idea of using the Poisson distribution to model recombination has a long history in genetics, going back to Haldane (1919). If we then imagine that this same process across all of the \(k\) individuals that connect you and one of your ancestors in the kth generation, the total number of breakpoints is a Poisson distributed, but with the rate is \(k\) times faster. Then, for a segment to survive to be passed from your ancestor in the kth generation to you, it must survive k independent coin flips—an event that occurs with probability ½k. By a nice property of Poisson processes known as Poisson thinning, this coin-flipping process can be incorporated directly into the Poisson process by changing it’s rate. Then, the expected number of segments \(N\) shared between you and your ancestor in the kth generation is:
\[\mathbb{E}[N] = \frac{1}{2^k}(22 + 33k)\]
where 33 is the total genetic length of the human autosomes in Morgans, a unit defined as the average number of recombinations that occur (and is named after the Morgan that created the figure above). The formula above can give us a good intuition about what’s going on—the number of segments created by recombination grows linearly with how far back we go (\(22 + 33k\)), but the survival probability decreases exponentially (½k). Using the Poisson distribution6, we can do more than just find an expression for the average number of segments you share with an ancestor, like calculate probabilities of sharing zero segments (such that your genealogical ancestor is not a genetic ancestor) and calculate the distribution of segment lengths. Additionally, these models can be easily extended to handle the segments shared between cousins.
What’s fascinating about this is that your may not share genetic material with your genealogical ancestors. If you play around with the equation above with different values of \(k\), you’ll see around \(k=9\) that you’re expected to share less than one segment with your ancestors 9 generations back. We can visualize this using an arc diagram, which depicts a present-day individual in the center as the white half-circle, your two parents, four grandparents, and so forth:
We see that one’s genetic ancestors don’t grow as rapidly one’s genealogical ancestors. There’s a lot more to say about this; see Graham’s terrific blog post on this topic for more information.
X Genealogies
In our paper, we were curious how these processes would play out on the X chromosome. The human genome contains 22 autosome pairs and one sex chromosome pair, give us 23 pairs (i.e. the 23 from 23andme), plus one mitochondrial genome. However, unlike the autosomes, the X chromosome undergoes a special inheritance pattern. Males have only one X chromosome, and a Y chromosome. In contrast, females have two X chromosomes. Each generation, individuals pass a haploid set of chromosomes to their offspring—meaning they take the 23 pairs and pass a combination of each pair. Since males have two different sex chromosomes (the X and the Y), these two different chromosomes don’t recombine like the autosomes (except for over a small region called the pseudo-autosomal region). Instead, the male either passes his X to a daughter or a Y to a son. Females, having two X chromosomes, do pass a recombined X chromosome to their son or daughter. Since the X can only recombine over its entire length in females, we call these female meioses recombinational meioses. Note that with the autosomes, every meiosis is a recombinational meiosis.
What’s fascinating is that this different inheritance pattern leads the X chromosome to have a different genealogy than the one’s biparental genealogy. Since males don’t pass X chromosomes to their sons, one’s X genealogy only includes a subset of one’s total ancestors, and is embedded inside of one’s total genealogy. Below is a genealogy for a present-day female, with her X genealogy shaded in:
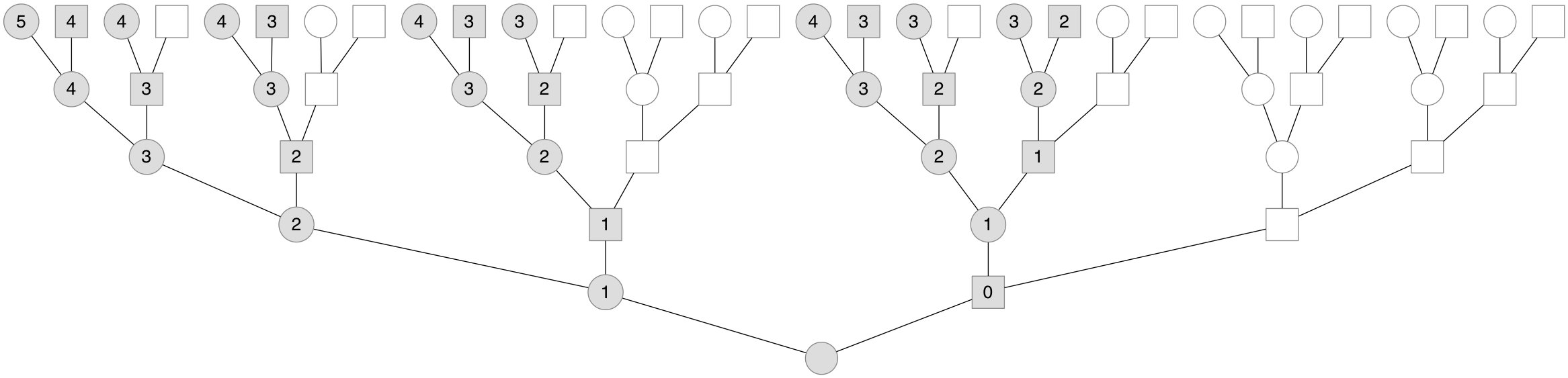
Note the number of X ancestors of a present-day female has back through the generations, 2, 3, 5, 8, etc. This sequence is the famous Fibonacci sequence offset by two. Thus, a present-female’s number of X ancestors is the \(k+2\) Fibonacci number, \(\mathcal{F}_{k+2}\) (if the present-day individual is a male, we offset this by one). This sequence crops up throughout nature and mathematics.
Models for X chromosome recent genetic ancestry
Another feature of X genealogies is that unlike the autosomes, where chromosomes undergo recombination every generation and in every ancestor, the number of X recombinational meiosis vary by lineage. This is because the number of females that occur in a lineage to an X ancestor in the 5th generation vary depending on the lineage. In the leftmost lineage of the genealogy above, a female occurs each generation. In contrast, the rightmost X lineage (with all shaded individuals) alternates between male and female ancestors. Since the X chromosome only undergoes recombination over its entire length in females, the specific lineage to an X ancestor impacts how quickly genetic relatedness breaks down. In our paper, we sought to characterize this lineage-specific rate and see how it affects genetic relatedness.
Our models are similar to the autosomal models described earlier, except given that we don’t know the particular lineage to an X ancestor, we need to average over the number of possible recombinational meiosis that could occur. We found that the number of lineages to an X ancestor \(k\) generations back with \(r\) recombinational meioses is:
\[{ r + 1 \choose k-r}\]
We can intuitively understand this by looking at an X genealogy; X genealogies enumerate every possible way to arrange males and females such that no two males are adjacent (since fathers don’t pass an X to their sons). Thus, the number of lineages \(k\) generations in the past with with \(r\) females can be thought of as the number of ways of ordering \(r\) red balls and \(k-r\) white balls such that no to white balls are adjacent. The number of ways of ordering red and balls this way is given by the binomial coefficient above.
Since one has \(\mathcal{F}_{k+2}\) X ancestors \(k\) generations back, the probability of \(r\) recombinational meioses occurring is:
\[P_R(R=r) = \frac{{ r + 1 \choose k-r}}{\mathcal{F}_{k+2}}\]
Averaging over this number of recombinational meioses gives us a model for the number and length of segments shared identically by descent on the X. It turns out the Poisson thinning approximation described earlier doesn’t work as well as another model we call the Poisson-Binomial model. I won’t cover the detailed derivation here (see the paper if you’re interested), but we find the distribution of X segment number to be well approximated by:
\[P(N=n \;|\; k, \nu) = \sum_{r=\lfloor k/2 \rfloor}^k \sum_{b=0}^\infty \text{Bin}(N=n \;|\; l=b+1, p=1/2^r) \; \text{Pois}(B=b \;|\; \lambda=\nu r) \; \frac{{r+1 \choose k-r}}{\mathcal{F}_{k+2}} \]
As with the autosomes, it’s possible one’s X genealogical ancestors don’t contribute X genetic material to their present-day descendent. For example, here is a simulated X genealogy with opacity of an ancestor indicating that ancestor’s genetic contribution to the present-day individual:
To get a sense of how one’s X genealogical ancestry grows back in time, we’ve plotted it below (Figure A) compared to one’s autosomal ancestry, and the growth of both one’s genetic X and autosomal ancestry back through the generations. Using probability models we work through in the next section, we also show (Figure B) the probability of sharing some autosomal genetic ancestry (P(Nauto > 0)) and X genetic ancestry (P(NX > 0), conditional and unconditional on both being an X genealogical ancestor (“X ancestor” and “ancestor”, respectively).
Similarly, we extend these models to model the number of X chromosome segments shared between half- and full-cousins and explore other properties of X cousins. These models get a bit tricky mathematically, as the sex of the cousins’ shared ancestor impacts the number of segments shared between cousins, so we incorporate the probability of the sex of the shared ancestor in our models (see Section 3 of our paper for more details).
What recent ancestry on the X can tell us
Using genetic data to infer relationships between individuals is an important topic—it’s used by services like 23andme for ancestry finding, in forensics in assessing DNA-based evidence, and in anthropology and ancient DNA to learn about the familial relationships among individuals. We were curious what X chromosome segments shared between cousins could tell us about their relationship. We found that X chromosome segments can be quite informative about which of their ancestors they share. This information occurs through two avenues: (1) sharing IBD segments on the X immediately reduces the potential genealogical ancestors two individuals share, since one’s X ancestors are only a fraction of their possible genealogical ancestors, and (2) the varying number of females in an X genealogy across lineages combined with the fact that recombinational meioses only occur in females to some extent leave a lineage-specific signature of ancestry. We’ll talk more about this second point in this section.
The X chromosome is relatively short (compared to the autosomes), leading ancestry signals to decay relatively rapidly. Thus, inferring how far back cousins share an ancestor is best accomplished through looking at segments shared on the autosomes rather than X chromosome, and many methods are available for this purpose (Durand et al., 2014; Henn et al., 2012; Huff et al., 2011). We condition on knowing how many generations back these half-cousins share a common ancestor using this autosomal signal. Then, we use Bayes theorem to invert \(P(N=n| R)\) to learn the posterior \(P(R | N=n)\), where \(R\) is the number of recombinational meioses (and thus number of females) between two half-cousins and \(N\) is the observed number of X segments shared between the cousins. These posterior distributions are:
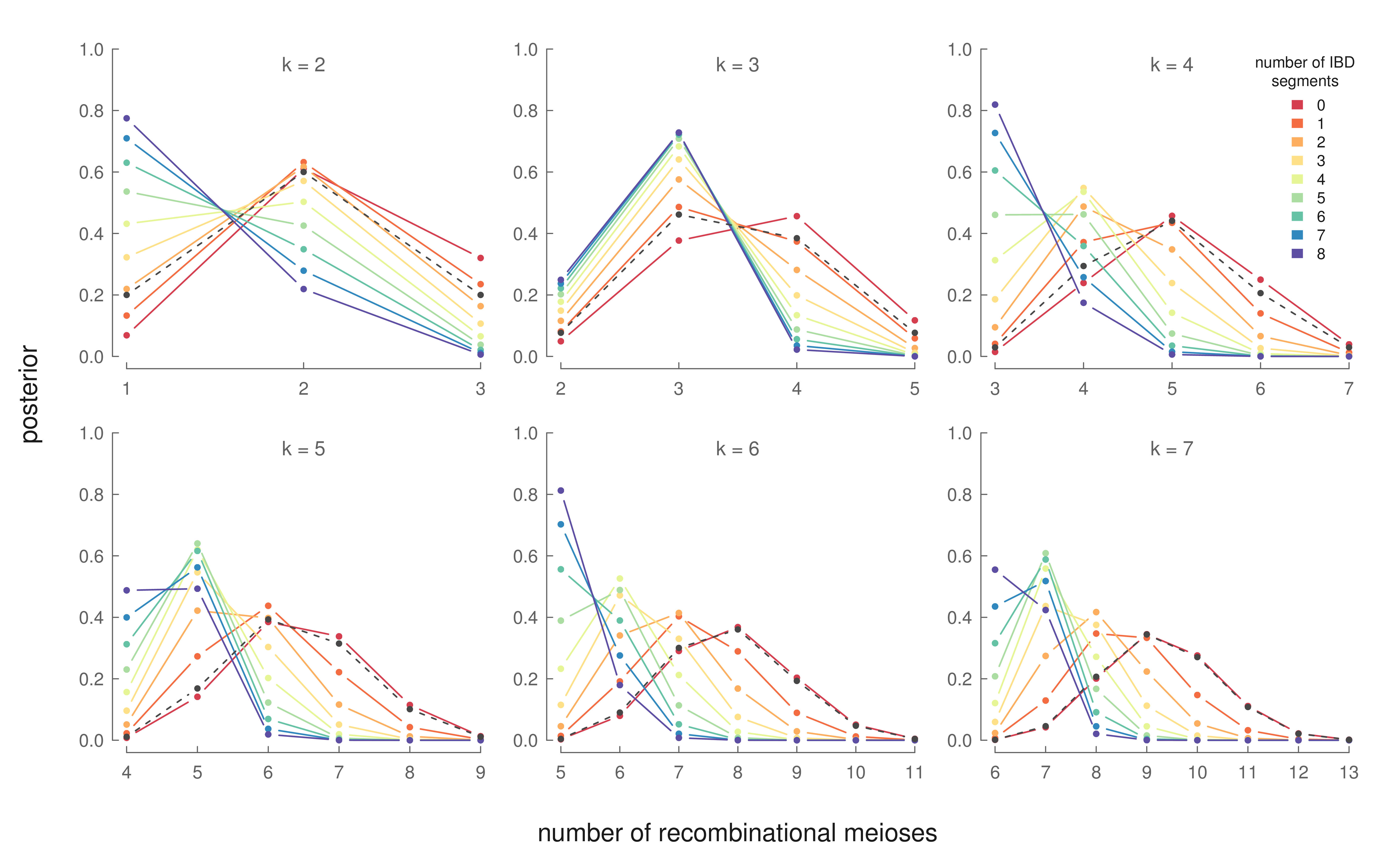
For example, the top right panel shows the posterior distributions for the number of females in the lineage connecting two 3rd degree half-cousins. Each line represents the posterior distribution for a specific number of observed segments shared between these two half-cousins. If these two 3rd degree cousins share six segments identically by descent, our models say that a lineage with three females is the most likely genealogical configuration. This information is interesting, as these genealogical details cannot be inferred with the autosomal data alone.
As genomic data sets increase, so will the probability of sampling individuals that share recent ancestry. With large data sets (e.g. 23andme’s users), there’s potential for recent ancestry on the X to shed some light on the genealogical relationships connecting us all.