Elucidating k-mer Contamination with Kullback-Leibler Divergence
Recently a coworker showed me a FASTQ file from an Illumina HiSeq run (which will be packaged in the new release of my Bioconductor package qrqc) that was severely contaminated. Below is the file in less with a string highlighted:
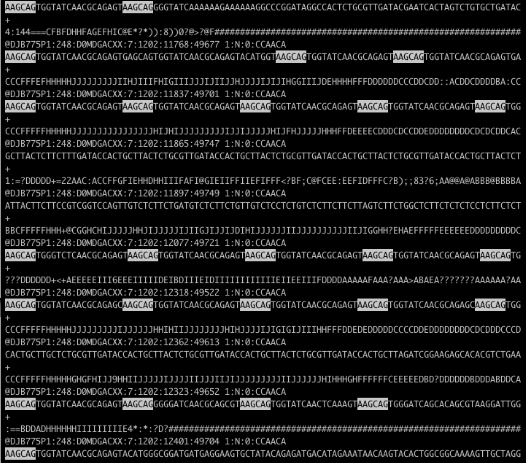
Holy contamination, Batman! There are a few approaches to handling this level of contamination. The program tagdust will match contaminated reads and remove them. My program Scythe is being changed so that it can match adapter contaminants further in the read using its Bayesian model. Both programs require a priori knowledge of possible contamiant sequences - what if this is a novel sequence contaminant? In this case, AAGCAGTGGTATCAACGCAGAGT appears to be a PCR primer related to DSN normalization that may not have made it into our adapter files.
k-mer Entropy Approaches
k-mer approaches are a nice way of searching for such contaminants. I am currently adding this feature to qrqc; you can follow development on the kmer branch on Github but this branch may merge into master and disappear.
The C functions I’ve written use Heng Li’s khash.h library to quickly hash k-mer sequences with their positions in the read. The end result is a data frame in R of k-mer sequence, position, and counts in that position.
Looking at raw k-mer counts is somewhat useful, but I’ve been exploring some information theoretical approaches to analyzing this data. One useful graphic is entropy of k-mers by position:
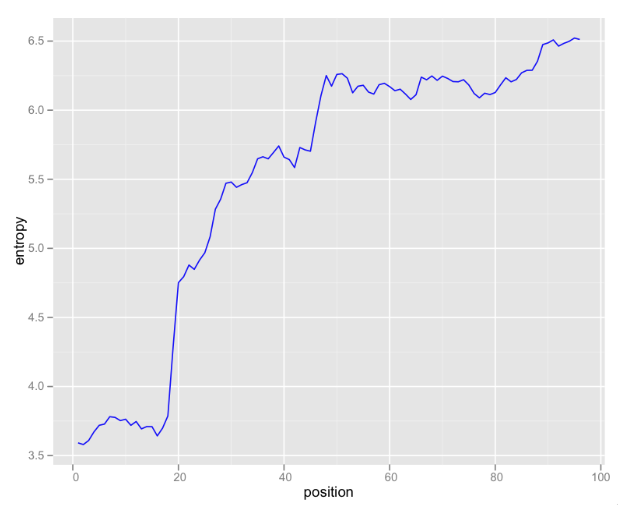
These are 6-mers, so there are 4,096 possible k-mers (excluding N). If the k-mer distribution were uniform, 12 bits would be needed to encode each k-mer. This graph illustrates that even at the most random 3’-end of the read, only about 6.5 bits are needed. In the first 20 bases, the distribution of k-mers is so skewed that less the Shannon entropy is less than four bits.
Kullback-Leibler Divergence Approach
It makes sense biologically that the k-mers don’t have uniform frequency. In the case of read contaminants, the enrichment by position against an empirical k-mer distribution may be as interesting as total k-mer enrichment against a random distribution model.
To assess this, some beta qrqc code pools k-mer counts across position to find an empirical k-mer distribution. Then, the k-mer distribution per position is compared to the pooled distribution using the Kullback-Leibler divergence. K-L divergence is only defined when both distributions sum to 1, the sample spaces are the same, and if \(q(i) > 0\) for any \(i\) such that \(p(i)> 0\).
In essence, the K-L divergence is measuring the average number of bits needed to encode data from P with a code based on the distribution of Q. In the k-mer case, Q is the empirical distribution of k-mers irrespective of k-mer position and P is the position-specific distribution of k-mers. Thus, an enrichment of k-mers at a particular position would lead to more divergence.
A nice feature of ggplot2 is the stacking of the “bar” geom. Since K-L divergences are sums, stacking and setting fill color by k-mer (the terms of the sum) gives us a sense of the total divergence and each k-mer’s effect on the total. There are too many k-mers to plot, so I have some procedures that find a nice subset. Because this is a subset, the K-L total (indicated by bar height) is wrong, but the graphical interpretation is easier. Now, the enrichment by position is clear:
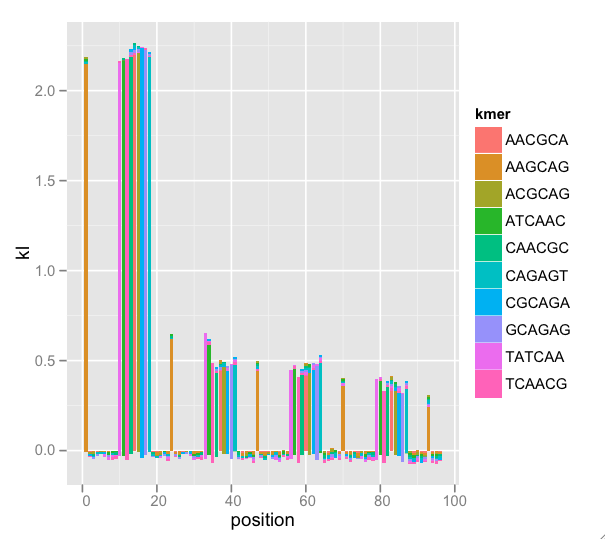
This messy dataset has repeat primer contamination. Note that because we’re plotting a subset of k-mers, there is negative total K-L (not mathematically possible) because we’re leaving out terms in the sum, but the meaning still comes through. Also note that there is k-mer nesting: The first wide peak begins with k-mer TATCAA, then ATCAAC, then TCAACG, etc. This indicates that we could adjust k and find the entire repeated k-mer.
Update
I’ve added faceting of multiple SequenceSummary objects’ KL/k-mer diagnostics. Combined with a random data file, this really illustrated contamination:
This is still in development; follow the code on Github and feel free to contact me and make suggestions.
